Динамические системы и их приложения

Теория динамических систем, являясь одним из активно развивающихся разделов современной математики, предоставляет мощную теоретическую базу для исследования самых разнообразных моделей, возникающих в естественных и социальных науках, в технике и технологиях. Сочетание внутреннего богатства и красоты результатов с исключительной практической важностью способствует привлечению все большего числа специалистов к изучению динамических систем.

Исследования, проводимые в Украине, играют немаловажную роль в развитии теории динамических систем. Еще в конце XIX века А. М. Ляпуновым были заложены основы современной теории устойчивости. В 30-40 годы ХХ века фундаментальный вклад в теорию динамических систем с инвариантной мерой и статистическую механику внес Н. Н. Боголюбов. Последующие исследования украинских математиков в этом направлении привели к созданию во второй половине ХХ века теории стохастических динамических систем, в частности, методов исследования асимптотического поведения многочастичных систем в случайных средах. В это же время были получены многообещающие результаты в топологической динамике одно- и маломерных динамических систем, а также в теории бесконечномерных систем, порождаемых разностными уравнениями с непрерывным временем и краевыми задачами математической физики.

Начиная с 60-х годов, Институт математики проводит конференции и школы, посвященные различным областям математики, в частности, и динамическим системам. Такие форумы оказали большое влияние на развитие не только теории динамических систем, но и нелинейной динамики в целом. Не так давно Институт математики принял решение регулярно проводить международные конференции “Динамические системы и их приложения” (ICDSA), нацеленные на укрепление сотрудничества и обмена достижениями в этой весьма актуальной области науки. Первая такая конференция, ICDSA-2012, состоялась в Киеве в 2012 году. Вторая конференция, ICDSA-2014, также состоится в Киеве. На ней будет рассмотрен широкий круг вопросов современной теории динамических систем, включая топологическую динамику, эргодическую теорию, теорию аттракторов и хаоса, комбинаторную и символическую динамику, теорию фракталов, бифуркации и теорию устойчивости, бесконечномерные динамические системы, различного рода приложения, особенно в математической физике. 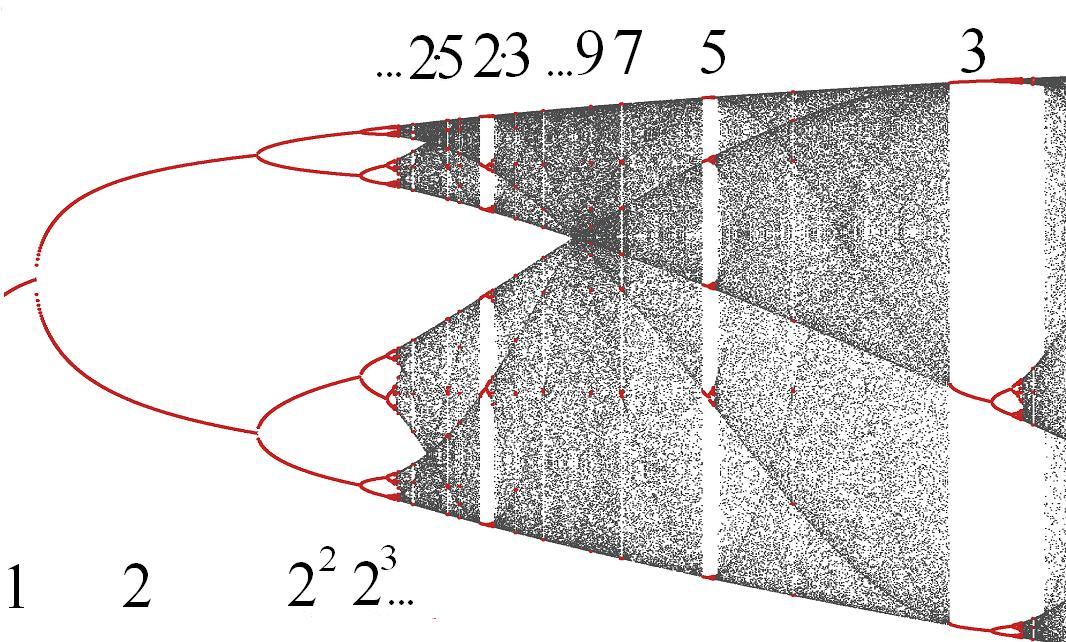Значительное внимание предполагается уделить комбинаторной динамике, берущей начало из широко известной теоремы о сосуществовании циклов, опубликованной в “Украинском математическом журнале” в 1964 году. В 1994 году в Испании состоялась международная конференция “Тридцать лет теоремы Шарковского: новые перспективы”, посвященная достижениям и новым проблемам в комбинаторной динамике, а в 2014 году комбинаторная динамика уже может отмечать свой 50-летний юбилей.